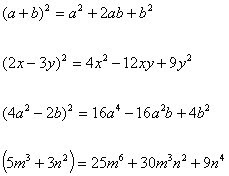FRACCION ALGEBRAICA
Se llama fracción algebraica al cociente de dos polinomios.

SIMPLIFICACION
Para simplificar una fracción, se factorizan numerador y denominador y se eliminan los factores comunes obteniéndose otra fracción equivalente.

OPERACIONES CON FRACCIONES ALGEBRAICAS

Suma y resta: Para sumar o restar fracciones algebraicas, estas se reducen a común denominador y se suman o restan los numeradores, dejando el mismo denominador. Después se simplifica la fracción resultante.

Producto : El producto de dos fracciones algebraicas es el producto de sus numeradores partido por el producto de sus denominadores.

Fracción inversa de otra : La fracción inversa de

es:

Cociente : El cociente de dos fracciones algebraicas es el producto de la primera por la inversa de la segunda (Producto cruzado de términos).

FACTORIZACION

El proceso inverso de desarrollar una multiplicación es la factorización . Factorizar quiere decir identificar a los factores comunes a todos los términos y agruparlos. Los factores comunes son aquellos números que aparecen multiplicando a todos los términos de una expresión algebraica. Estos números pueden estar dados explícitamente o representados por letras.
Así, factorizar un polinomio, es descomponerlo en dos o más polinomios llamados factores, de tal modo que al multiplicarlos entre si se obtenga el polinomio original. Algunos ejemplos:

De la expresión podemos factorizar b

y obtenemos la expresión: .... ( 1 )

Veamos paso a paso cómo se obtuvo la expresión:

ahora podríamos reacomodar la expresión que queda dentro del paréntesis:

Finalmente si sustituímos este último resultado en (1), obtenemos:

PRODUCTOS NOTABLES

Se llama productos notables a ciertas expresiones algebráicas que trabajando se las encuentra uno frecuentemente y es preciso saber factorizarlas a simple vista, es decir, sin necesidad de hacerlo paso por paso.

· BINOMIO AL CUADRADO

Es igual al trinomio cuadrado perfecto. Y se obtiene de la siguiente manera:

Cuadrado del primer término.
Más el doble producto del primer término por el segundo.
Más el cuadrado del segundo término.

Ejemplo:

FACTORIZACION DE UN TRINOMIO CUADRADO PERFECTO

Extraemos raíz cuadrada al primer y tercer términos del trinomio.
Con estas raíces formamos un binomio que tendrá el signo del segundo término del trinomio.
Este binomio será la raíz cuadrada del trinomio y deberá multiplicarse por sí mismo o elevarse al cuadrado.

Ejemplo:

· BINOMIOS CONJUGADOS

Binomios conjugados da como resultado diferencia de cuadrados.

Cuadrado del primer término menos
El cuadrado del segundo término.

Ejemplos:

FACTORIZACION DE UNA DIFERENCIA DE CUADRADOS

Se extrae la raíz cuadrada al primer y segundo términos.
Se multiplica la suma de estas raíces por su diferencia.

Ejemplo:



· BINOMIO AL CUBO

El cubo del primer término más
El triple del cuadrado del primer término por el segundo más
El triple del primer término por el cuadrado del segundo más
El cubo del segundo término.

Ejemplos:

· PRODUCTO DE BINOMIOS CON TERMINO COMUN

El producto de estos binomios es igual a un trinomio de la forma

Cuadrado del término común, más
El producto de la suma algebraica de los no comunes por el común, más
El producto de los no comunes.

Ejemplos:

FACTORIZACION DEL TRINOMIO

El primer término de ambos factores será la raíz cuadrada del primer término.
Los dos términos que faltan deben cumplir con las condiciones que siguen:

v Su producto debe ser igual al tercer término del trinomio
v La suma algebraica de estos ha de ser igual al coeficiente del segundo término del trinomio.

OPERACIONES BASICAS CON POLINOMIOS

OPERACIONES BÁSICAS CON POLINOMIOS

· SUMA Y RESTA

Solo se pueden sumar y restar cosas iguales, por ejemplo: manzanas con manzanas; metros con metros; pesos con pesos, etc.

Los ejemplos anteriores se relacionan con el hecho de que sólo se pueden sumar o restar términos que sean semejantes.

SUMAR: significa que respetes el signo de cada término que se coloca después del símbolo de suma.

RESTA: significa que debemos cambiar por el inverso aditivo el coeficiente del término que está después del símbolo de resta.

EJEMPLOS:

(3x+4y-5z) + (-3y+3z+x)

Primero se identifican los términos semejantes

Después se realiza ya sea suma o resta para obtener el producto final

RESULTADO: 4x+y-2z

(-2b+4c-5a) + (-a+2b+2c)= -6a+6c

· PRODUCTO

1. Se multiplicará cada término del primer polinomio por el otro polinomio.
2. Se tendrá en cuenta los signos para que el resultado sea el adecuado.

EJEMPLOS:

(2x-3y) ()= -

Se multiplica primero el 2x por los términos del otro polinomio y después el -3y

() ()= -

· COCIENTE

Para resolver este tipo de divisiones es necesario el uso de la galera, pues no existe otra forma posible para su resolución.

1. Ordenar el dividendo (va dentro de la galera), según las potencias descendentes (de mayor a menor) de una misma literal que aparezca en ambos polinomios.
2. Si el dividendo no cuenta con todas sus potencias continuas, debemos dejar un espacio en blanco en donde éstas falten.
3. Para obtener el primer termino del cociente, dividimos el primer termino del dividendo entre el primer termino del divisor.
4. Multiplicamos este primer término del cociente por todo el divisor y se resta algebraicamente del dividendo.
5. El residuo obtenido se trata como un nuevo dividendo y se repiten los pasos 3 y 4.
6. Continuamos con este proceso, hasta que en el residuo el exponente de la literal que escogimos sea menor que el exponente de la misma literal en el divisor.

NOTA: LA VERDAD NO LE PUDE REPRESENTAR NINGÚN EJEMPLO PORQUE ESTABA UN POCO DIFÍCIL DE HACERLO, PERO CREO QUE EL PROCEDIMIENTO ES MUY ENTENDIBLE.

CANTIDADES PROPORCIONALES

Se le llama proporción a la igualdad de dos razones (el cociente de dos números enteros), y se dice que las cantidades que intervienen en una proporción son proporcionales. Por ejemplo:
Medios
O bien 2 : 3 :: 4 : 6

Extremos

Esta proporción se lee: dos es a tres (2 : 3) como (::) cuatro es a seis (4 : 6)

Cuando en una proporción desconocemos una de las cuatro cantidades, podemos encontrar el valor de esta cantidad aplicando la regla de que el producto de los medios es igual al producto de los extremos.

EJEMPLOS:

1.

= 2 : 3 :: X : 6 (3) (X) = (2) (6)




Debemos despejar la incógnita, es decir; pasarla sola a un lado de la igualdad; el 3 esta multiplicando a nuestra cantidad desconocida, por lo que pasa dividiendo al otro miembro de la igualdad.

2.

(2) (6) = (X) (4)


3.

X : 10 :: 24 : 8


4.

X : 4 :: 25 : X (X) (X) = (4) (25)

X= 10

Para eliminar el exponente debemos sacar la raíz cuadrada a ambos miembros de la igualdad; esto se hace para que no se altere la igualdad.

PROPORCION DIRECTA

Dos cantidades son directamente proporcionales a otras dos, cuando la razón de las dos primeras es igual a la razón de las dos últimas.
Esto significa que si aumenta una de las cantidades entonces aumenta la otra y viceversa.

EJEMPLOS:

1. Si compramos 5 refrescos por 10 pesos y queremos saber el costo de solo uno, ¿cuesta más de 10 pesos o menos?

5 refrescos es a 1 refresco como 10 pesos es a X pesos

5 : 1 :: 10 : X

X=2 por lo tanto 1 refresco costará 2 pesos

2. si cuatro cuadernos de dibujo nos cuestan 26 pesos y queremos saber el costo de dos, ¿qué debemos hacer?

Planteamos la proporción directa:

4 : 2 :: 26 : X

= 13 2 cuadernos cuestan 13 pesos

PROPORCION INVERSA

Dos números son inversamente proporcionales a otros dos cuando la razón de los primeros es igual a la razón inversa de los últimos.
En otras palabras, dos cantidades son inversamente proporcionales cuando una decrece si la otra aumenta.

EJEMPLOS:

1. Si 4 carpinteros terminan un trabajo en 10 días, 8 carpinteros lo terminarán ¿en menor o mayor tiempo?

Al aumentar el número de carpinteros se reduce el tiempo que necesitan para concluir el trabajo: mas carpinteros requieren menos tiempo.

El planteamiento de la proporción es el mismo:

4c : 8c :: 10d : Xd o bien

Esta vez la solución no es la misma ya que si se resuelve como vimos anteriormente en proporciones directas el resultado nos saldrá mayor. Por lo tanto se invierte el orden en que escribimos la proporción en la que se encuentra la incógnita.

Ahora podemos resolverlo aplicando la noción de que el producto de los extremos es igual al producto de los medios:

De esta manera sabemos que los carpinteros terminaran su trabajo en 5 días.


REGLA DE TRES

Este es un método aritmético que da solución a operaciones en las cuales se conocen tres, de cuatro cantidades, relacionadas entre si proporcionalmente, y que nos permite encontrar el valor de la cantidad desconocida.

EJEMPLOS:

1. Si 20 lápices cuestan 60 pesos, ¿Cuánto cuestan cinco lápices?

Lápices (l) pesos ($)

20 60
5 X

2. Si un poste de cuatro metros de altura proyecta una sombra de 1.2 metros y en el mismo instante un edificio proyecta una sombra de 3.6 metros, ¿Qué altura tiene el edificio?

Alturas (m) sombras (m)

4 1.2

X 3.6


3. si 4 obreros terminan una excavación en 48 horas, ¿en cuanto tiempo la terminarían 6 obreros?

Obreros (o) tiempo (h)

4 48

6 X




PORCENTAJES

A menudo los resultados en razones y proporciones se relacionan con porcentajes (tanto por ciento), ya que esta es otra forma de expresar qué parte es una cosa de otra.
El porcentaje de una unidad determinada simboliza las partes que se toman de esta como si estuviera dividida en 100 partes iguales.

EJEMPLOS:

1. Si una tarea la terminamos en 50 minutos y hasta este momento llevamos solo 25 minutos de trabajo, ¿Qué porcentaje de trabajo hemos realizado?


Esta razón indica la parte de la tarea que ya hemos realizado. Pero como el porcentaje considera el total dividido en 100 partes iguales, entonces el porcentaje es la razón de 25 a 50, expresada como parte equivalente de 100, por lo que esta razón debe multiplicarse por 100.


2. En la clase de matemáticas hay 50 alumnos, y solo 35 de ellos aprobaron, ¿qué porcentaje de alumnos reprobaron?

Tenemos que restar los 50 alumnos a los 35 que pasaron para obtener la cantidad de alumnos que reprobaron:

La cantidad de alumnos reprobados es 15 ahora podemos sacar el porcentaje:

El 30% de los alumnos reprobó

3. En el primer semestre de bachillerato hay 500 alumnos y sabemos que 15% de ellos reprobaron la asignatura de matemáticas. ¿Cuántos alumnos reprobaron la asignatura?

Podemos resolver este problema por medio de una regla de tres:

Alumnos porcentaje

500 100%
X 15%


MÍNIMO COMÚN MÚLTIPLO

1.- Encontrar el mínimo común múltiplo de 2, 6, 12
1er método
Se genera los múltiplos de cada uno
M(2) ={0,2,4,6,8,10,12,14,16,…}
M (6) = {0, 6, 12, 18, 24, 30,36,…}
M (12) = {0, 12, 24, 36,48,…}
Como el mínimo común múltiplo es aquel múltiplo que es común a todos, pero que además es mínimo de todos sus múltiplos, en este caso observamos que el múltiplo que cumple con dicha condición es 12 ya que es múltiplo de común a 2, 6 y 12
2do método
Se colocan los tres números en fila y se encuentra el mínimo múltiplo a los tres y se divide cada uno por ese múltiplo, colocando el múltiplo a la derecha de los resultados de las divisiones

2

6

12

MCM
1
3
6
2

Se observa si se han generado algún 1, de generarse se busca el múltiplo de los que aun no se ha generado 1, en este caso buscaremos uno que divida a 3 y a 6, observamos que 3 divide a 3 y a 6 por lo que, el tres se coloca de bajo de la palabra MCM, por debajo del 2.

2

6

12

MCM
1
3
6
2

1
2
3
Finalmente nos falta dividir 2 el cual es divisible entre 2

2

6

12

MCM
1
3
6
2

1
2
3

1
1
2
Observamos que 2 se divide por si mismo, por lo tanto

2

6

12

MCM
1
3
6
2

1
3
3

1
2
2


1
1

Observamos que 2 se divide por si mismo, por lo tanto el mínimo común múltiplo es el producto de la columna por de bajo de MCM=2X3X2X1=1X22X3=12


MÁXIMO COMÚN DIVISOR
El máximo común divisor de dos o más números naturales esta definida como el número que divide a todos los números que intervienen, pero que además es máximo divisor.
EJERCICIOS:
Encontremos el mínimo común múltiplo de 6, 10, 12
6 se puede dividir por 2, 3 y 6
10 se puede dividir por 2, 5 y 10
12 se puede dividir por 2, 3, 4, 6,12
El divisor que tienen en común es 2 en este caso es el único, pero de no serlo debemos de pensar en el divisor común, pero que además se el máximo.
Otra forma se genera de la siguiente forma
6
2
3
3
1

6=2x3
Los divisores para 10
10
2
5
5
1

10=2x5
Los divisores para 12
12
2
6
2
3
3
1

Como el MCD se forma de todos los de menor potencia, en este caso el Maximo Común Divisor es: 212=22x3

2. Encontrar el máximo común divisor de 90,35 y de 15
Veamos la descomposición de 90
90

2
45
3
15
3
5
5
1

Por lo que 90=2x32x5
Para 35 tendremos
35

5
7
7
1

35=5x7
Para 15 tendremos
15

3
5
5
1

15=3x5


Por lo tanto el máximo común divisor es 5

TIPOS DE INTERÉS

Imagínese que dos personas A y B invierten al mismo tiempo un capital C, con una misma tasa de interés i. Al cabo de un año, A retira los intereses producidos por el capital y vuelve a dejar el mismo capital invertido. En el segundo año vuelve a retirar los intereses y a invertir el mismo capital, y así cada año. Cada año retira los intereses producidos durante ese año y reinvierte sólo el capital C. En cambio B, al cabo del primer año no retira el interés sino que lo invierte junto con el capital anterior durante un año más, y así sucesivamente.

Interés simple e interés compuesto

El interés simple es el que se obtiene cuando los intereses producidos, durante todo el tiempo que dure una inversión, se deben únicamente al capital inicial. En el ejemplo anterior, el interés de la persona A es un interés simple.
Interés compuesto es el que se obtiene cuando al capital se le suman periódicamente los intereses producidos. Así al final de cada periodo el capital que se tiene es el capital anterior más los intereses producidos por ese capital durante dicho periodo. El interés de B en el ejemplo anterior es un interés compuesto.

Fórmula del interés simple

El interés que produce un capital es directamente proporcional al capital inicial, al tiempo que dure la inversión, y a la tasa de interés:
Donde i está expresado en tanto por uno y t en años.
Ejercicio: Calcular a cuánto asciende el interés producido por un capital de 25 000 pesos invertido durante 4 años a una tasa del 6% anual.
Resolución: Al expresar el 6% en tanto por uno, se obtiene que i = 0.06. Y por consiguiente,
El interés es de 6 000 pesos.
Ejercicio: Calcular el interés simple producido por 30 000 pesos durante 90 días a una tasa de interés anual de 5%.
Resolución: Como
Por tanto
Ejercicio: Al cabo de un año, un banco ha ingresado en una cuenta de ahorro 970 pesos por concepto de intereses. La tasa de interés de una cuenta de ahorro es del 2% anual. ¿Cuál es el saldo medio (capital) de dicha cuenta en ese año?
Resolución: Despejando C de la fórmula
Se obtiene que
El saldo medio ha sido de 48 500 pesos.
Ejercicio: Un préstamo de 20 000 pesos se convierte al cabo de un año en 22 400 pesos. ¿Cuál es la tasa de interés cobrada?
Resolución: Los intereses han ascendido a
Y despejando i obtenemos
.
La tasa de interés es del 12%.
Ejercicio: Un capital de 300 000 pesos invertido a una tasa de interés del 8% durante un cierto tiempo ha generado unos intereses de 12 000 pesos. ¿Cuánto tiempo ha estado invertido?
Resolución: Aplicando la fórmula, se tiene que
Y despejando
Por lo que el tiempo que ha estado invertido es de 0.5 años, es decir, 6 meses.
Fórmula del interés compuesto
Sea un capital invertido durante años a una tasa de interés compuesto por cada año. Durante el primer año el capital C produce un interés
El capital final al primer año será:
Después del segundo año, el capital C1 produce un interés
El capital final al segundo año será:
Y así sucesivamente.
Al cabo de n años el capital inicial C invertido en la modalidad de interés compuesto se convertirá en un capital final dado por la fórmula
Puesto que el interés generado es la diferencia entre el capital final y el inicial, se obtiene
La tasa de interés i se obtiene despejando en la fórmula de Cn
Aunque las fórmulas de interés compuesto se han deducido para una tasa de interés anual durante años, todo sigue siendo válido si los períodos de reinversión son semestres, trimestres, etc., sin más que convertir éstos en años.
Ejercicio: Averiguar en qué se convierte un capital de 1 200 000 pesos al cabo de 5 años y a una tasa de interés compuesto anual del 8%.
Resolución: Aplicando directamente la fórmula de Cn
Ejercicio: Un cierto capital invertido durante 7 años a una tasa de interés compuesto anual del 10% se ha convertido en 1 583 945 pesos. Calcular el capital inicial sabiendo que los intereses se han pagado semestralmente.
Resolución: Como los intereses se han pagado semestralmente, la fórmula que hay que aplicar es:
Y sustituyendo obtenemos
Y despejando C obtenemos
Ejercicio: Calcular la tasa de interés compuesto anual que se ha aplicado a un capital de 1 500 000 pesos para que al cabo de 4 años se haya convertido en 2 360 279 pesos.
Resolución: Se tiene
Y por consiguiente
La tasa de interés ha sido del 12%.